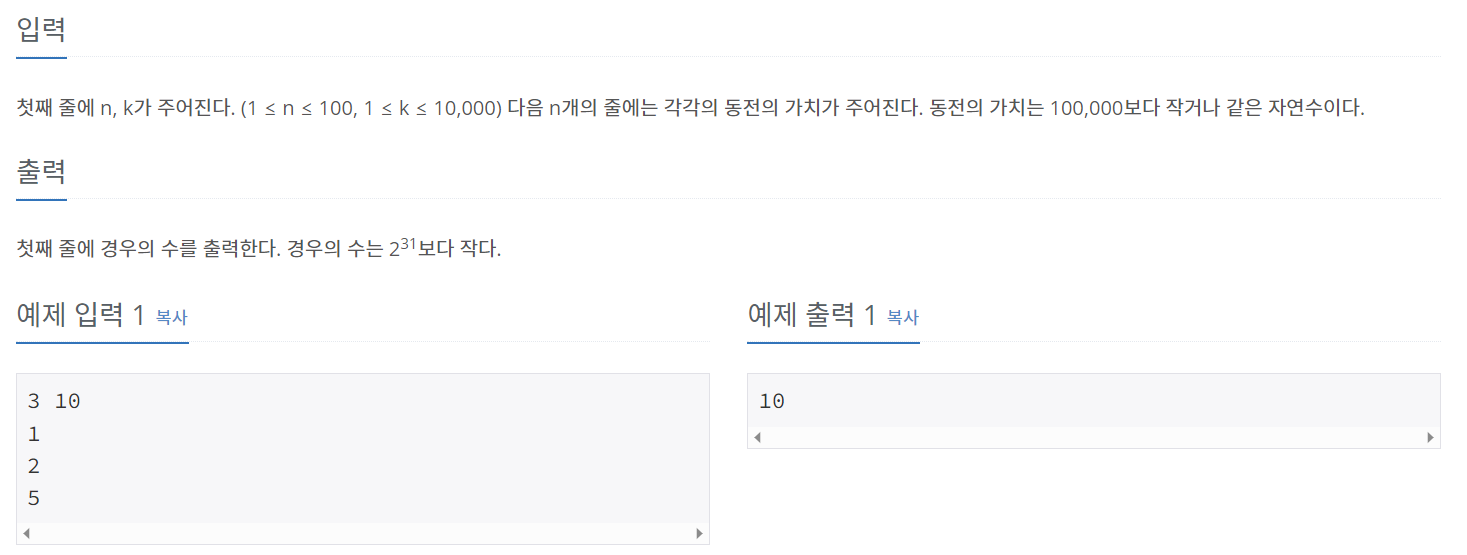
<입력>

<입출력>
<풀이>
이전에 풀던 문제는 다이나믹 프로그래밍을 이용해 최소 개수나 최대 개수를 구하는 것이었는데, 이 문제는 경우의 수를 구하라는 면에서 달랐다. 다이나믹 프로그래밍을 이용해 어떻게 값을 저장해야 좋을지 고민하였다.
가치 k가 되는 경우의 수 문제를 가치 i (1 <= i <= k)가 되는 경우의 수를 구하는 문제로 세분화 하여 값을 저장하였다.
즉, dp =[0] * (k+1) 을 만들어 dp[ i ] 번째의 값은 i가 될 수 있는 경우의 수이다.
예시를 적용해보면,
1. 가치가 1인 동전만 사용하는 경우,
dp [1] = dp[2] = dp [3] = dp[4] ... =1
2. 가치가 1, 2 인 동전을 사용하는 경우,
2원인 동전을 사용하지 않는 경우는 1번에서 구했으므로 더해주지 않아도 된다.
2원인 동전을 사용하는 경우는 점화식을 이용해서 더해준다.
<코드>
n, k = map(int, input().split())
coin = []
for i in range(0, n):
coin.append(int(input()))
dp = [0] * (k+1)
dp[0] = 1
for c in coin:
for i in range(c, k+1):
dp[i] = dp[i] + dp[i-c]
print(dp[k])
<결과>

'코딩 테스트 > 다이나믹 프로그래밍' 카테고리의 다른 글
| [백준 11722번] 가장 긴 감소하는 부분 수열 문제 풀이 with Python (0) | 2023.08.22 |
|---|---|
| [백준 11049번] 행렬 곱셈 순서 문제 풀이 (0) | 2023.08.21 |
| [백준 2579번] 계단 오르기 문제 풀이 (0) | 2023.08.02 |
| [백준 15486번] 퇴사 2 문제풀이 (0) | 2023.07.31 |
| 다이나믹 프로그래밍 개념 (0) | 2023.07.23 |




댓글